Una función es el resultado de realizar ciertas operaciones matemáticas, las cuales pueden contener una o más variables y el resultado de esas operaciones será el valor de la función. Para ilustrar esto vamos a definir una función sencilla que consistirá en multiplicar un valor por dos. La operación será 2·x, siendo x el valor de la variable que se multiplica y la función la podemos llamar funcion(x), que significa función cuyo valor depende de x, por tanto funcion(x)= 2·x. Otra sencilla función puede ser la suma de dos números x + y, y por tanto, la función sería f(x,y)=x + y, que significa que la función f, depende de los valores que introduzcamos en las variables x e y.En Descartes, detrás del nombre de la función, va un paréntesis y, separadas por comas, las variables de las que depende. Las funciones, por tanto, asignan un número real a cada valor de su variable (o a cada conjunto de valores de sus variables). Las funciones tienen un identificador (o nombre), una o más variables (que no son más que una lista de identificadores y que van detrás del nombre entre paréntesis) y una expresión o conjunto de operaciones en la que pueden intervenir una o más variables.
Estos son ejemplos de funciones de una variable con sus identificadores y sus variables:
|
expresión |
identificador (nombre de la función) |
variable |
| f(x)=sen(3*x+2) | f | x |
| g(y)=A*exp(-(y^2)/(s^2)) | g | y |
| Area(radio)=(pi*radio^2)/2 | Area | radio |
Estos son ejemplos de funciones de dos o más variables con sus identificadores y sus variables:
|
expresión |
identificador (nombre de la función) |
variable |
| f(x,y)=raíz(x^2+y^2) | f | x,y |
| Fun(x,y,z) | Fun | x,y,z |
| Volumen(a,b,c)=4*pi*a*b*c/3 | Volumen | a,b,c |
Los nombres específicos de las variables de una función sirven para identificar las variables dentro de la expresión y asignarles allí un papel. Las funciones se evalúan (es decir, se obtiene el valor de las mismas) sólo cuando son llamadas explícitamente (por ejemplo, por un algoritmo, por un gráfico, por una variable de texto, por la animación o por la constricción de un control gráfico que se mueve), es decir, desde algún punto o instrucción de la escena se pide que la función se realice y muestre su valor, para llamar a una función se pone su nombre seguido de un paréntesis con las variables de las que depende, por ejemplo, f(x) o Fun(x,y,z). Una función puede llamarse desde cualquier otra función, desde un algoritmo o desde la animación y al llamarla no hay que asignarla a una variable, basta escribir su nombre y los parámetros que se le pasan separados por comas y entre paréntesis.
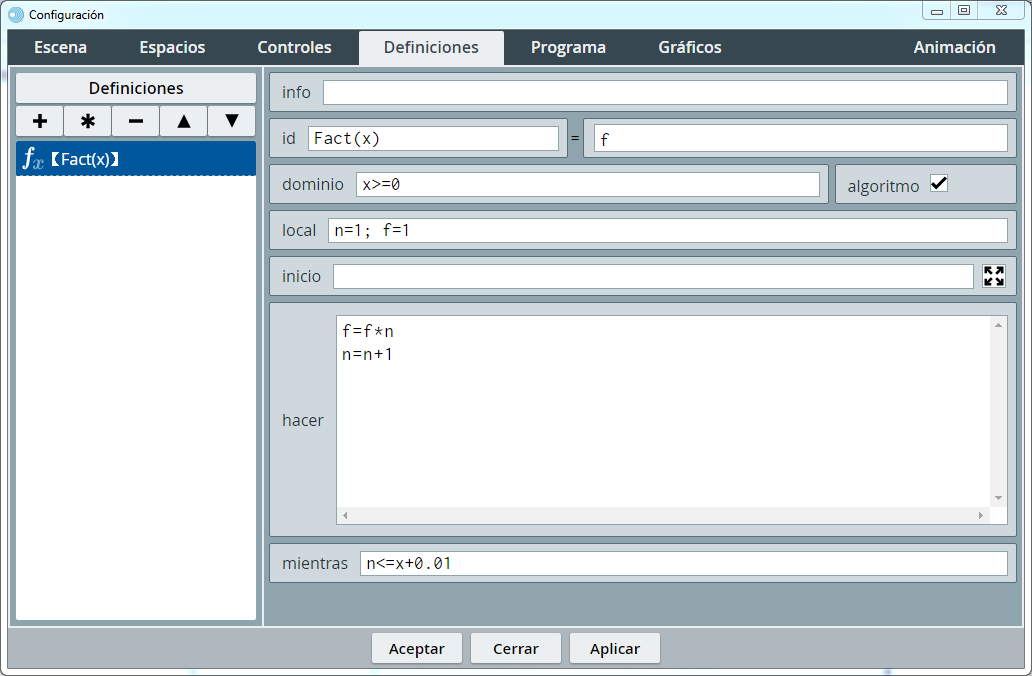
El panel de configuración de una función tiene este aspecto y su configuración se detalla en la siguiente tabla:
|
id (definición de la función, nombre, variable y operaciones)
|
Consta de dos campos de texto. En el primero se especifica el identificador o nombre de la función y debe incluir los parámetros de los que dependa escritos entre paréntesis y separados por comas. Por ejemplo: f(x, y, z).
En el segundo se detalla una expresión que será el valor a asignar como imagen a esa función, por ejemplo, x + y + z. |
|
dominio |
Es una expresión booleana (condicional) que determina el dominio de la función.
Cualquier intento de evaluar la función fuera de su dominio lanzará una excepción, con lo cual, por ejemplo, su gráfica no se dibuja en los puntos que no están en el dominio. El valor por defecto es vacío, lo cual se interpreta como que el dominio no está restringido. Cuando el programa intenta evaluar una función en un punto donde tiene una singularidad, se genera una interrupción, igual que si el punto no estuviera en el dominio. Por lo tanto, no es necesario excluir del dominio de una función sus puntos singulares, el programa ya lo hace automáticamente. Sólo hay que especificar el dominio si se desea restringir el dominio natural de una función. |
|
algoritmo |
Selector que indica si la función, para evaluarse, debe usar un algoritmo; es decir, si necesita los cálculos indicados en "inicio", "hacer" y "mientras".
|
|
inicio
|
En el campo "inicio" puede escribirse una serie de asignaciones y llamadas a algoritmos separadas por punto y coma (;).
Todo lo que haya en este campo se ejecuta al inicio del cálculo. |
|
local
|
En este campo se introducen variables que sólo van a ser utilizadas dentro de la función. Si hay más de una variable a proteger dentro de la función, se debe separar por punto y coma (;).
|
|
hacer
|
En el campo "hacer" puede escribirse una serie de asignaciones y llamadas a algoritmos separadas por saltos de línea.
Lo que hay en "hacer" se ejecuta repetidamente mientras la condición "mientras" sea válida. |
|
mientras
|
En el campo "mientras" se debe escribir una expresión booleana (condicional).
Lo que hay en "hacer" se ejecuta repetidamente mientras la condición "mientras" sea válida. |
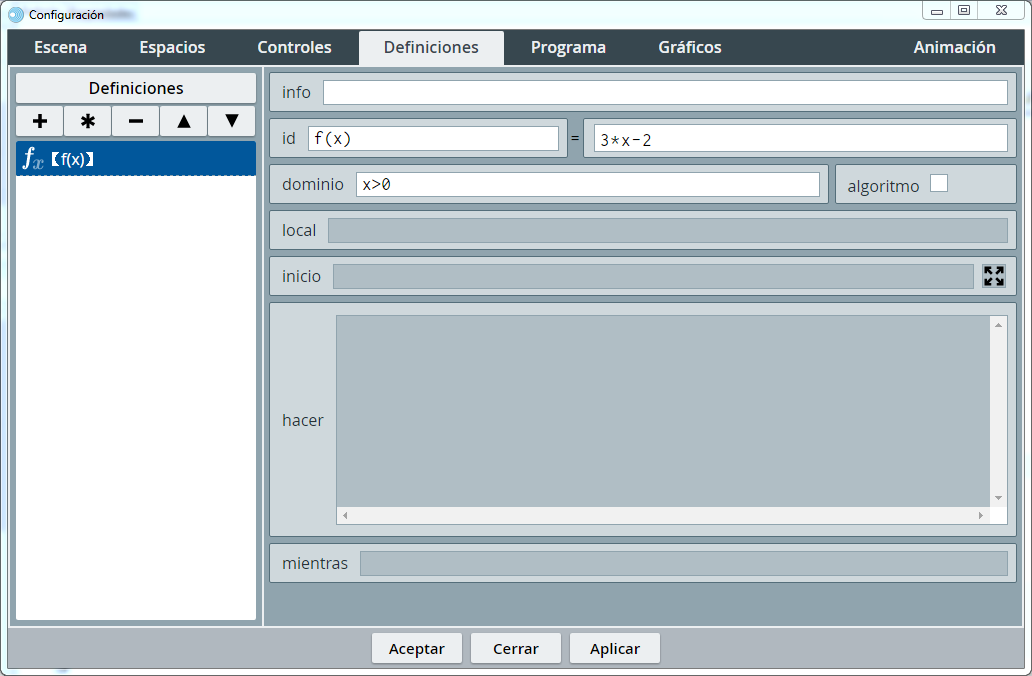
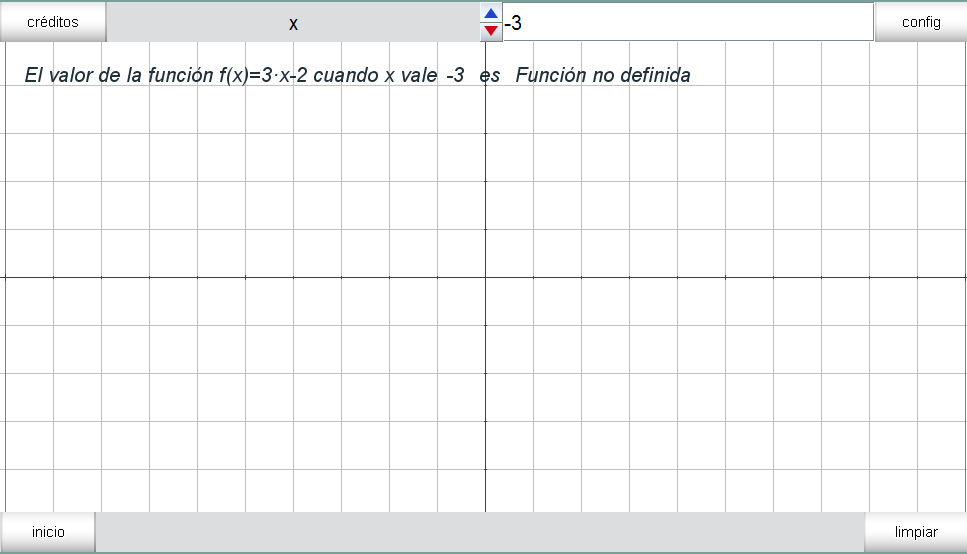
Vamos a insertar una función sencilla, por ejemplo, la función multiplicar por tres un número y restar dos, la operación sería 3*x-2, y a la función la podemos llamar f(x), y pediremos que esta función sólo se evalúe para valores positivos de x, es decir su dominio será x>0.
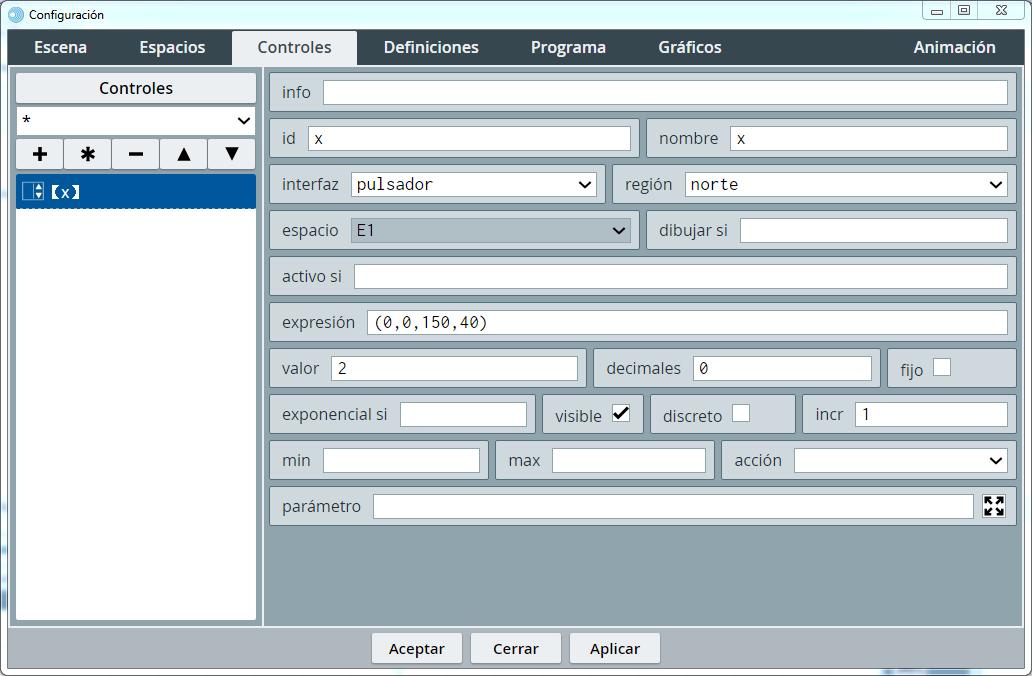
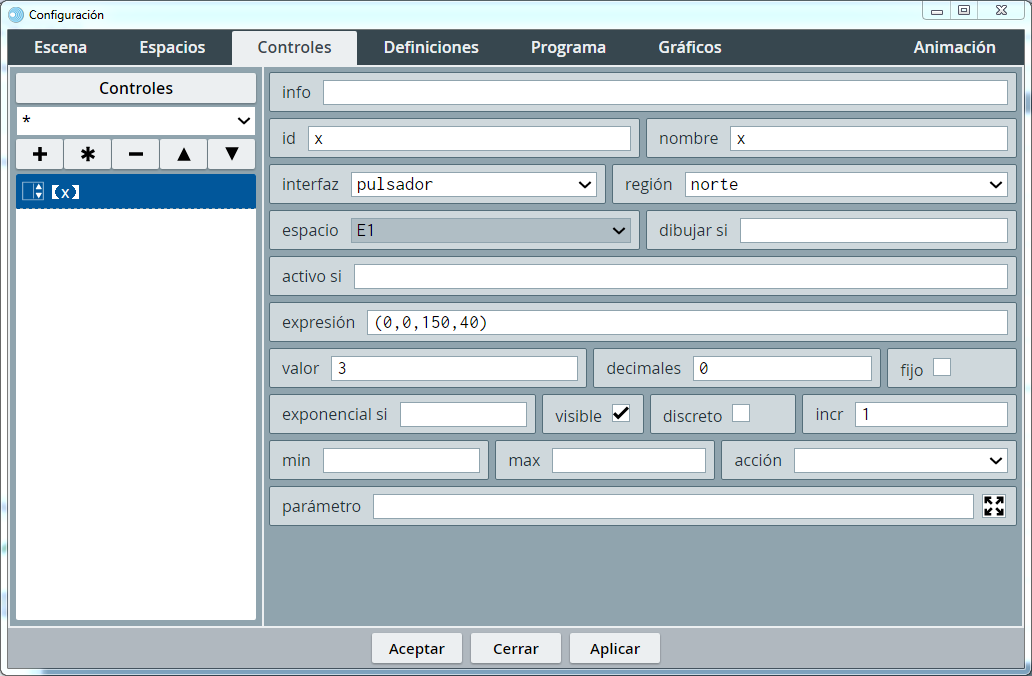
Vamos a insertar un control numérico tipo pulsador en la región norte que le de valores a la variable x.
Finalmente insertaremos un texto con formato en el que se llame a la variable x y a la función f(x), la función al ser llamada por el texto se ejecuta y muestra su valor. Recordamos que la variable x y la función f(x) se introducen pulsando en el menú superior de la ventana de texto con formato primero en [F] y después en ex, mostrándose en pantalla [expr]. Al pulsar sobre [expr] se abre una ventanita que nos permite meter la variable x y la función f(x). Esto ya se ha explicado anteriormente y se explica con detalle al final de este apartado.
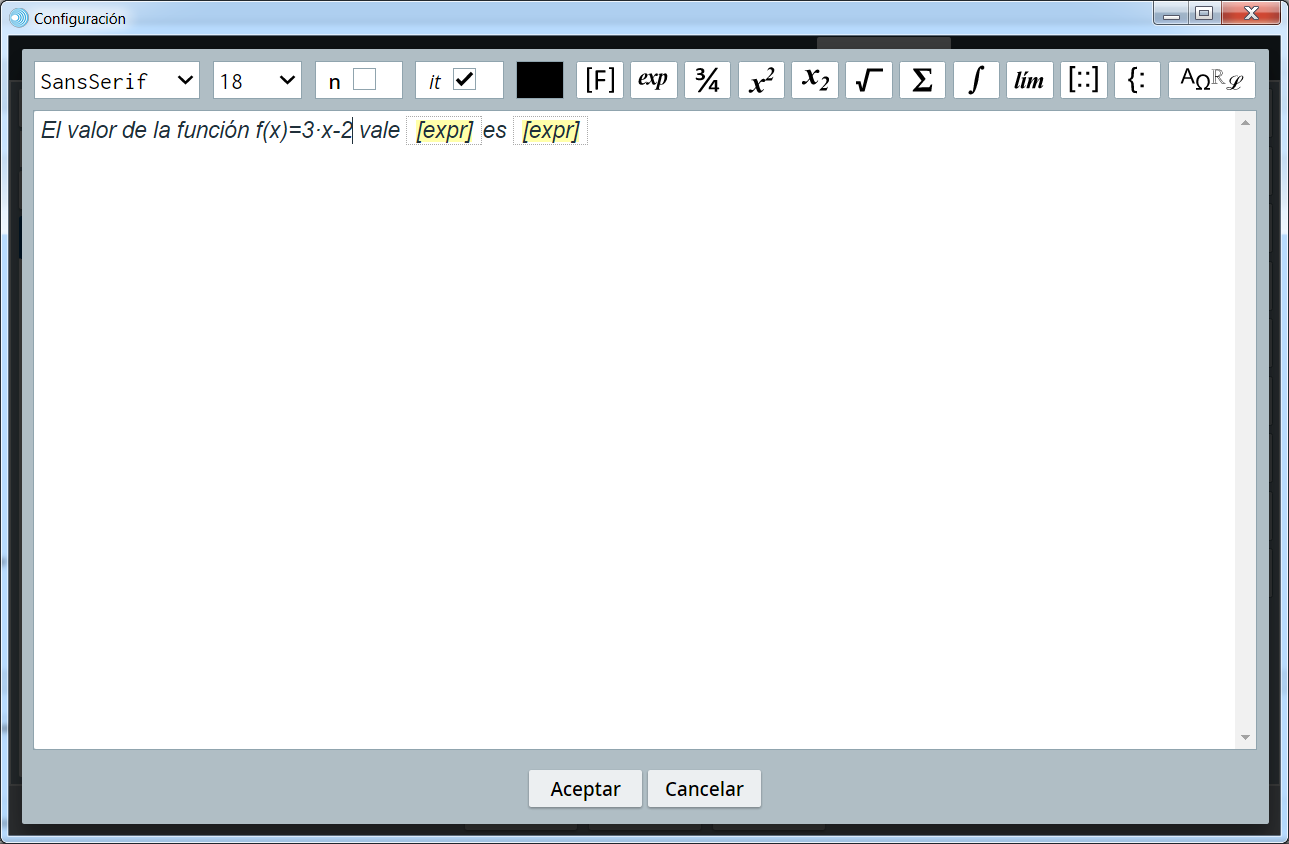
Dependiendo del valor de x que se ponga en el control obtendremos un valor de la función f(x).
Sin embargo, si x toma valores negativos, la función no estará definida, ya que en el dominio hemos indicado que la función sólo debe tomar valores cuando x sea positiva y se mostrará lo siguiente:
Vamos a insertar un control numérico tipo pulsador en la región norte que le de valores a la variable x.
A veces no se puede definir una función solamente mediante una expresión, sino que su evaluación requiere un proceso más complicado. En estos casos el autor puede marcar el campo algoritmo, con lo cual la evaluación de la función realiza antes el algoritmo definido en los campos de texto etiquetados con inicio, local, hacer y mientras (en inicio se pueden asignar valores iniciales a variables o funciones, en local las variables internas de la función, hacer repetirá la operación indicada hasta que deje de cumplirse la condición indicada en el campo mientras, si este campo se deja en blanco hacer se ejecutará una sala vez). En estos campos el autor puede describir el algoritmo de evaluación de la función.
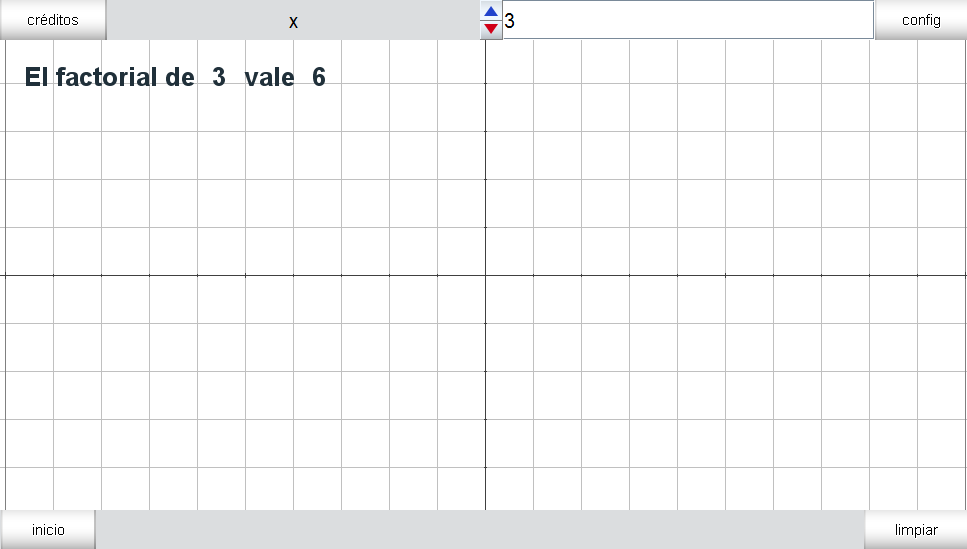
El siguiente ejemplo muestra cómo puede una función utilizar un algoritmo. Se trata de la función factorial (matemáticamente consiste en multiplicar el número al que se realiza el factorial por todos los menores enteros positivos que él, por ejemplo, el factorial de 4 será 4·3·2·1=24, el factorial de 5 valdrá 5·4·3·2·1=120). En nuestra escena definiremos la función Fact(x) (función que depende del valor de la variable x, que calcula el factorial del número x, que por definición deberá ser entero y positivo, por lo que su dominio deberá de ser x>=0.
Pasamos a explicar cómo funciona el algoritmo de la función Fact(x) cuyo valor será el de f. En inicio se asigna a las variables n y f el valor de 1. En hacer, se realizará las operaciones f=f*n y n=n+1, mientras n<=x+0.01. Calcularemos el factorial de 3, es decir x=3.
- En el primer ciclo de hacer f=1 y n=1, por lo que f=1*1=1 y n=1+1=2. La condición mientras: n<=x+0.01 se sigue cumpliendo ya que 2<=3+0.01, por lo que se ejecutará otro ciclo de hacer.
- En el segundo ciclo de hacer f=1 y n=2, por lo que f=1*2=2 y n=2+1=3. La condición mientras: n<=x+0.01 se sigue cumpliendo ya que 3<=3+0.01, por lo que se ejecutará otro ciclo de hacer.
- En el tercer ciclo de hacer f=2 y n=3, por lo que f=2*3=6 y n=3+1=4. La condición mientras: n<=x+0.01 ya no se cumple ya que 4 no es menor que 3+0.01, por lo que el algoritmo parará. En este punto f=6, que es el valor del factorial de tres.
Finalmente insertaremos un texto en el que se llame a la variable x y a la función Fact(x), la función al ser llamada por el texto se ejecuta y muestra su valor.
donde las [expr] son las casillas donde introduciremos las variables y las funciones (recordemos que para que salga [expr] hay que pulsar en el menú superior de la ventana de textos con formato en las teclas [F] y ex en este orden). Al pulsar sobre [expr] se abre una ventanita en la que pondremos x y en otra la función Fact(x).
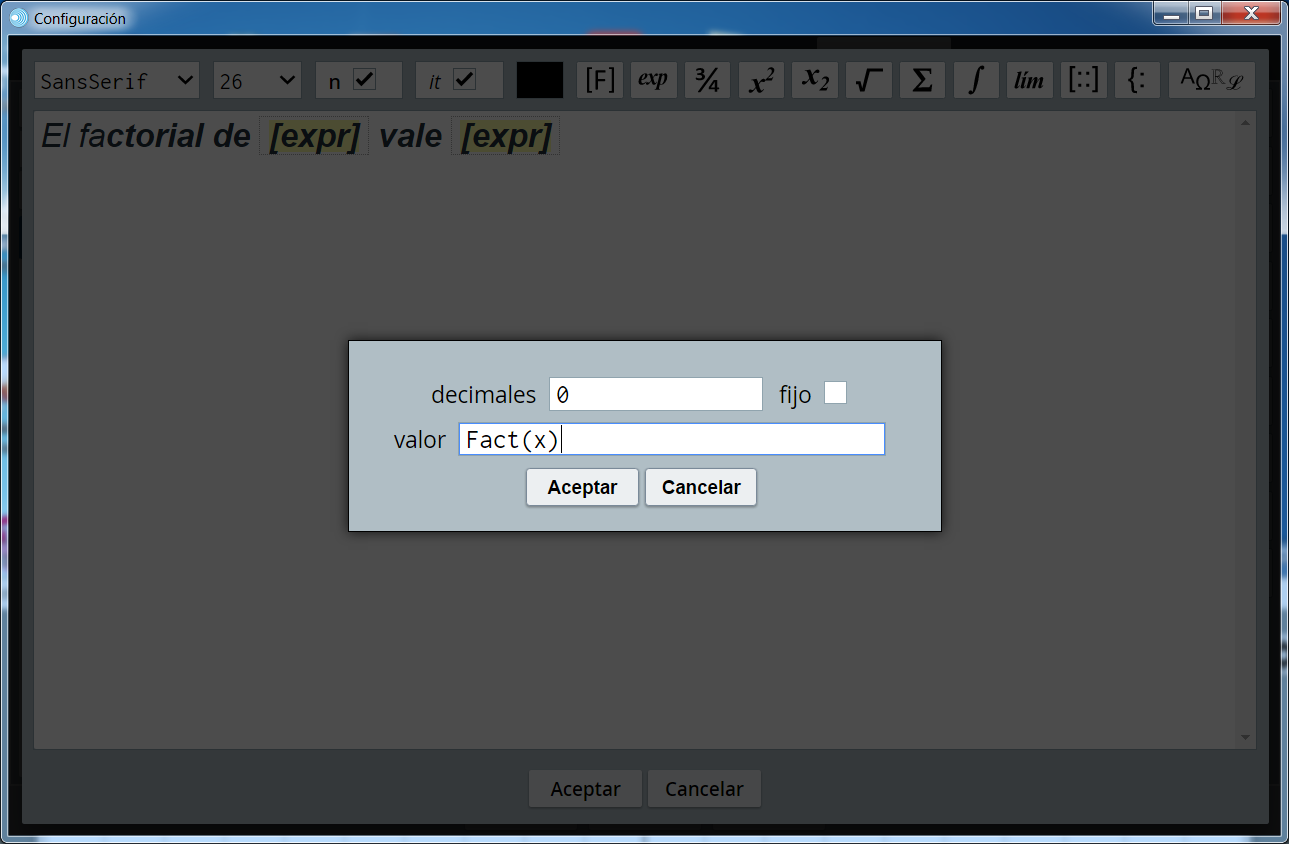
Dependiendo del valor de x que se ponga en el control obtendremos un valor de la función Fact(x).
Las funciones también pueden utilizar operadores condicionales o booleanos para definirse. La expresión que aparece a la derecha del signo = puede ser, o incluir, un término condicional.
Ejemplo: func(x)=(x<0)?0:1, donde func es una función que vale 0 para (x<0) y 1 para (x>=0).
Una expresión booleana vale 1 cuando es verdadera y 0 cuando es falsa por lo cual la función anterior también podría escribirse como: func(x)=(x>=0)